১৯৯০ সালের দিকে রন রাইভেস্ট হ্যাশ ফাংশন এর কন্সেপ্ট ব্যবহার করে Message Digest 4 ( MD4 ) নাম এ একটি এলগরিদম ডিজাইন করেন । ১৯৯২ সালের দিকে এই এলগরিদম কে বর্ধিত করে আরেকটি এলগরিদম বানান যেটার নাম হয় Message Digest 5 ( MD5 ) । পরবর্তীতে ১৯৯৩ সালে National Institute of Standards and Technology (NIST) MD5 এর সাথে মিল রেখে একটি এলগরিদম তৈরি করেন । এটাই Secure Hash Algorithm বা SHA-0 নামে পরিচিত । তবে এই আলগরিদমটি অতটা শক্তিশালি না হওয়ায় ১৯৯৫ সালে এটার ই নতুন ভার্সন আসে যেটা SHA-1 নামে পরিচিত ।

The steps of SHA-1

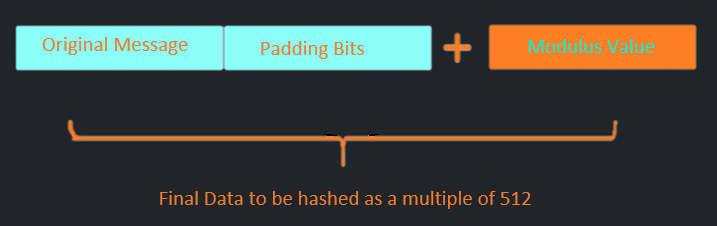
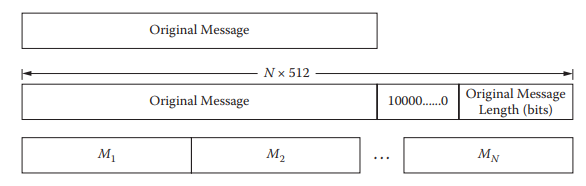
১। ম্যাসেজ কে হ্যাশ করার আগে আমরা ম্যাসেজ এর দৈর্ঘ্য দেখব । যদি ম্যাসেজ এর দৈর্ঘ্যকে ৫১২ দিয়ে মড করলে ৪৪৮ হয় তাহলে আমাদের প্যাডিং করা লাগবে না । আর যদি এমন না হয় তাহলে আমরা ম্যসেজকে প্যাডিং করব । প্যাডিং শুরু হবে ১ থেকে আর বাকি অংশটুকুতে ০ থাকবে । শেষ ৬৪ বিট খালি থাকবে । এই বিটগুলো অরিজিনাল ম্যাসেজ এর লেন্থ স্টোর করতে ব্যবহৃত হয় । 

 SHA-1 ১৬০ বিটের একটি ম্যাসেজ ডাইজেস্ট তৈরি করে যেটা ৫ টি ৩২ বিটের ওয়ার্ড এ বিভক্ত । ধরি ৫ টি বিট হচ্ছে h0,h1,h2,h3 এবং h4 । এগুলোকে নিচের মান দিয়ে ইনিশিয়ালাইজ করা হয় – 

h0 = 0x67452301

h1 = 0xefcdab89

h2 = 0x98badcfe

h3 = 0x10325476

h4 = 0xc3d2e1f0

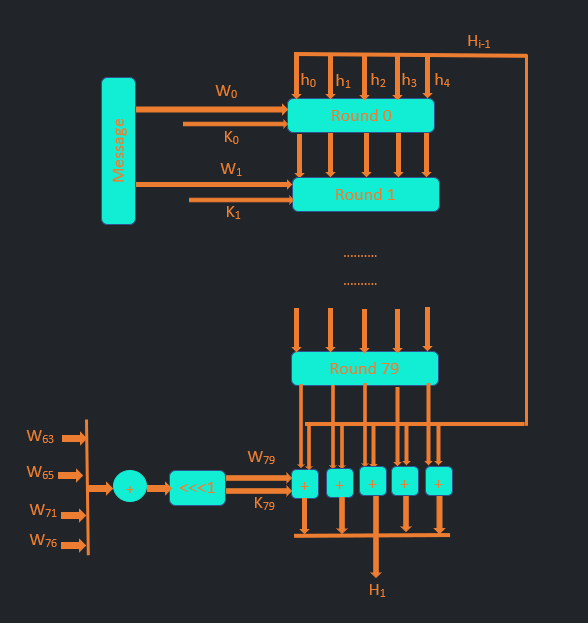
এখানে মান গুলোকে বিগ এন্ডিয়ান ফরম্যাট এ রাখা হয় । বিভিন্ন ধাপের মধ্যে দিয়ে যাওয়ার সময় এদের মান পরিবর্তিত হয়ে যায় ।  SHA-1  এ ৮০ টা রাউন্ড হয়ে থাকে । ০ থেকে ৭৯ পর্যন্ত । ৭৯ রাইন্ড এর পর h0,h1,h2,h3 এবং h4  এর যেউ মান টা পাওয়া যায় সেটাই আমাদের কাংখিত ম্যাসেজ ডাইজেস্ট । 

২।ম্যাসেজ প্রসেসিংঃ

আমরা জানি যে প্রতিটা ম্যাসেজ কে ৮০ টি রাউন্ড এর মধ্যে দিয়ে যেতে হয় । ৮০ টি রাউন্ড এর মধ্যে দিয়ে যেতে হলে h0,h1,h2,h3 এবং h4 এ আমরা ০-১৫ পর্যন্ত যেতে পারব । এর পরের মানগুলা আমাদের নিচের ফরম্যাট এ বের করতে হবে । 

Wi = W(i-3) + W(i-8) + W(i-14) + W(i-16) 

Wi কে তারপর এক ঘর বামে রোটেট করা হয় এবং একটা কন্সট্যান্ট Ki এর সাথে পরবর্তী রাউন্ড এ নেওয়া হয় । এখানে K এর মান রাউন্ড অনুসারে পরিবর্তিত হয় । 

Ki  =  0x5a827999 ( 0  ≤  t  ≤  19)

Ki  =  0x6ed9eba1 ( 20  ≤  t  ≤  39)

Ki  =  0x8f1bbcdc ( 40  ≤  t  ≤  59)

Ki = 0xca62c1d6  ( 60  ≤  t  ≤  79)

সাধারণত প্রথম রাউন্ড বাদে প্রতিটি রাউন্ডেই আগের রাউন্ডের থেকে ১৬০ বিটের ( ৫ ওয়ার্ড )  এর বাফার ভ্যালু দরকার হয় । প্রথম রাউন্ডের টা কীভাবে ইনিশিয়ালাইজ করতে হয় সেটা আমরা আগে আলোচনা করেছি । সবগুলো অপারেশনই একটি রাউন্ডের মাধ্যমে করা হয় যেটা নিচের ছবিতে আমরা দেখব । প্রতিটি রাউন্ড এক একটা ফাংশন তৈরি করে যেটা আমরা নিম্নোক্তভাবে দেখিঃ

A = h(i − 1, 1)

B = h(i − 1, 2)

C = h(i − 1, 3)

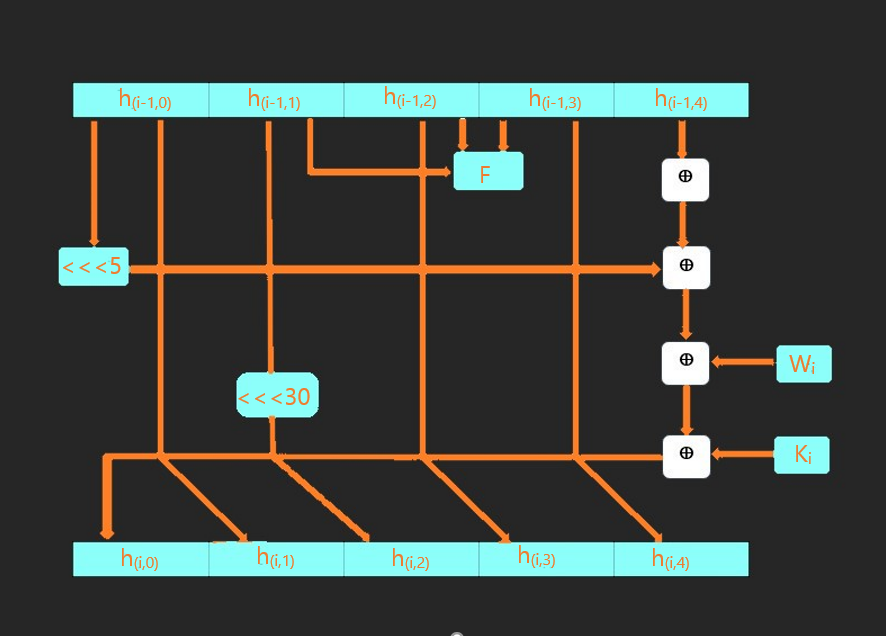
F= f( i, A, B, C) = ( A ^ B ) v ( -A ^ C )                                            [0<=i<=19]

                         = ( A ⊕ B ⊕ C )                                                    [20<=i<=39]

                         = ( A ^ B ) v ( A ^ C ) v ( B ^ C )                            [40<=i<=59]

                         = ( A ⊕ B ⊕ C )                                                   [60<=i<=79]

নিম্নোক্ত উপায়েও একটা ফাংশন বের করা যায় 

h(i,1) = h(i-1,0)

h(i,2)=LS30(h(i-1,1))

h(i,3)=h(i-1,2)

h(i,4)=h(i-1,3)

h(i,0)=(((h(i-1,4)⊕F)⊕LS5(h(i-1,0)))⊕Wi⊕)Ki

যেখানের LSi  j বিটের নাম্বার কে রোটেট করছে বাম দিকে যেখানে i একটি পূর্ণসংখ্যা ।

এবং শেষপর্যন্ত আমরা ১৬০ বিটের একটা ফাইনাল হ্যাশ ভ্যালু পাইঃ

Hi = sum ( H(i-1) , 79 ) 

এভাবে প্রতিটা রাউন্ডে হ্যাশ ভ্যালু আপডেট হতে হতে ফাইনালি আমরা যে মানটা পাই সেটাই আমাদের কাঙ্ক্ষিত হ্যাশ ভ্যালু ।

নিচে আমরা একটা উদাহরণের মাধ্যমে দেখব । 

ধরি আমরা যেই ম্যাসেজটা কে ডাইজেস্ট করব সেটা হলোঃ 

M = “The quick fox jumps over the lazy dog” . 

এটাকে বিট এ কনভার্ট করলে হয় 

01010100 01101000 01100101 00100000 01110001 01110101 01101001 01100011 0110101100100000 01100110 01101111 01111000 00100000 01101010 01110101 01101101 0111000001110011 00100000 01101111 01110110 01100101 01110010 00100000 01110100 0110100001100101 00100000 01101100 01100001 01111010 0111100100100000 01100100 0110111101100111 00101110

এখানে মোট ৩০৪ টি বিট আছে । এটাকে যাতে ৫৫২ দিয়ে মোড করলে ৪৪৮ আসে তার জন্য আমরা এটাকে আরো ১৪৪ বিটের প্যাডিং করব । অতএব আমরা প্যাডিং এর পর পাব 

01010100 01101000 01100101 00100000 01110001 01110101 01101001 01100011 0110101100100000 01100110 01101111 01111000 00100000 01101010 01110101 01101101 0111000001110011 00100000 01101111 01110110 01100101 01110010 0010000001110100 0110100001100101 00100000 01101100 01100001 01111010 01111001 00100000 01100100 0110111101100111 00101110 10000000 00000000 00000000 00000000 00000000 00000000 0000000000000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 0000000000000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 0000000 100110000 

এই ম্যাসেজটা এখন ১৬ ভাগে বিভক্ত করব আমরা ( ০ থেকে ১৫ পর্যন্ত ) যার প্রথম ৩২ বিট আমরা W০ এ আর শেষ ৩২ বিট আমরা W১৫ এ রাখব । এবার আমরা SHA-1 এর প্রক্রিয়া অনুযায়ী ম্যাসেজ গুলো এনক্রিপ্ট করব । আগেই আলোচনা করেছি যে ১৬০ বিটের বাফার এ আমাদের এই ম্যাসেজ গুলো রাখতে হবে । তো প্রথমেই আমরা ১৬০ বিট এর বাফারগুলো ইনিশিয়ালাইজ করব ।

h0: 00000001 00100011 01000101 01100111 

h1: 10001001 10101011 11001101 11101111 

h2: 11111110 11011100 10111010 10011000

h3: 01110110 01010100 00110010 00010000 

h4: 11110000 11100001 11010010 11000011 

রাউন্ড ০ এর পর এগুলো হবে 

h0: 11010011 11111101 00011100 11110100

h1: 00000001 00100011 01000101 01100111 

h2: 11100010 01101010 11110011 01111011 

h3: 11111110 11011100 10111010 10011000 

h4: 01110110 01010100 00110010 00010000

রাউন্ড ১ এর পর এগুলো হবে 

h0: 11101110 11110000 11000101 01011011 

h1: 11010011 11111101 00011100 11110100 

h2: 11000000 01001000 11010001 01011001 

h3: 11100010 01101010 11110011 01111011 

h4: 11111110 11011100 10111010 10011000

রাউন্ড ২ এর পর এগুলো হবে

h0: 10110001 00100101 00001111 00110011

h1: 11101110 11110000 11000101 01011011 

h2: 01110100 00111111 00000111 11111101 

h3: 11000000 01001000 11010001 01011001 

h4: 11100010 01101010 11110011 01111011

রাউন্ড ৩ এর পর এগুলো হবে

h0: 01111010 00111101 10010000 00001001 

h1: 10110001 00100101 00001111 00110011 

h2: 00111011 01111100 11110001 10010110 

h3: 01110100 00111111 00000111 11111101 

h4: 11000000 01001000 11010001 01011001 

রাউন্ড ৪ এর পর এগুলো হবে

h0: 00101111 00100011 11001101 00110001 

h1: 01111010 00111101 10010000 00001001 

h2: 01101100 11001001 11000011 01001100 

h3: 00111011 01111100 11110001 10010110 

h4: 01110100 00111111 00000111 11111101 

. 

.

.

রাউন্ড ৭৯ পর এগুলো হবে

h0: 10100110 11101101 10001111 00011011

h1: 11011100 01010111 10011001 10111010 

h2: 01000000 01000111 11111110 00000110 

h3: 01000011 11001000 00111000 00101110 

h4: 00010100 00111010 00100010 11100001

যেহেতু ম্যাসেজ প্যাডিং এর লেন্থ ৫১২বিটের কম তাই হ্যাশিং এক ব্লকেই হয়ে যাবে । ফাইনালি আমরা যেই হ্যাশিং টা পাব ওটা হবে রাউন্ড ৭৯ এর ম্যাসেজ অর্থাৎ

h0: 10100110 11101101 10001111 00011011

h1: 11011100 01010111 10011001 10111010 

h2: 01000000 01000111 11111110 00000110 

h3: 01000011 11001000 00111000 00101110 

h4: 00010100 00111010 00100010 11100001

এটাকে হেক্সাডেসিমাল এ প্রকাশ করলে হয় 82d510a7aa6703659fb9243e3e6b1cb9a4f51c04 যা আমাদের কাঙ্ক্ষিত ডাইজেস্ট । 

SHA-1 কে সবচেয়ে শক্তিশালি এলগরিদমগুলোর মধ্যে একটা ধরা হয় । তবে ২০০৫ সালে এর উপর ক্রিপ্টানালাইসিস করে দেখা গেলো যে এটি থিওরেটিকাল যতটা শক্তিশালি প্রাক্টিকালি এটা ততটা কার্যকারিতা দেখাতে পারে না । তাই পরবর্তীতে ২০১০ সালে SHA-2 প্রস্তাব করা হয় ।  

নিচে এর পাইথন কোড দেওয়া হলোঃ

        
import hashlib

def sha1_hash(message):
    # Create a new SHA-1 hash object
    sha1 = hashlib.sha1()

    # Update the hash object with the bytes-like object (message)
    sha1.update(message.encode('utf-8'))

    # Get the hexadecimal representation of the digest
    hashed_message = sha1.hexdigest()

    return hashed_message

# Example usage:
message = "Hello, World!"
hashed_message = sha1_hash(message)
print(f"Original message: {message}")
print(f"SHA-1 hash: {hashed_message}")