AES পার্ট-১ এ আমরা এনক্রিপশন- ডিক্রিপশন অ্যালগরিদম দেখেছি। এই পার্টে আমরা দেখবো পূর্ববর্তী পার্টের সেগমেন্ট-D এর key expansion সেগমেন্টটুকু কীভাবে কাজ করে। 

AES-128  key expansion অ্যালগরিদম 128 বিটের একটা key ইনপুট হিসেবে নেয় এবং সেটাকে 4×4 ম্যাট্রিক্সে রূপান্তর করে। ম্যাট্রিক্সের প্রতিটি সেলের সাইজ ১ বাইট এবং প্রতিটি কলামের সাইজ ১ ওয়ার্ড। কিন্তু AES এনক্রিপশন অ্যালগরিদমের ইনিশিয়াল ট্রান্সফরমেশন এবং ১০টি রাউন্ডের প্রতিটিতে 4 ওয়ার্ডের একেকটি key ব্যবহৃত হয়, তার মানে 4 ওয়ার্ডের ইনপুট key থেকে আমরা 44 ওয়ার্ডের একটা অ্যারে বানাবো, যাতে এনক্রিপশনের ধাপগুলোতে আমরা 4 ওয়ার্ড করে ইনপুট দেওয়ার মতো পর্যাপ্ত  key বানাতে পারি । 

অ্যালগরিদম :

        
 KeyExpansion (byte key[16], word w[44])
{
    word temp 
   for (i=0; i <4; i++)
   {
   w[i] = (key[4*i], key[4*i+1], key[4*i+2], key[4*i+3])
   }

   for(i = 4; i<44; i++)
   {
      Temp = w[i-1]
      if (i mod 4 = 0){
      temp = SubWord(ShiftWord(temp)) ⊕ Rcon[i /4] }
    w[i] = w[i-4] ⊕ temp 
   }
}
        
    

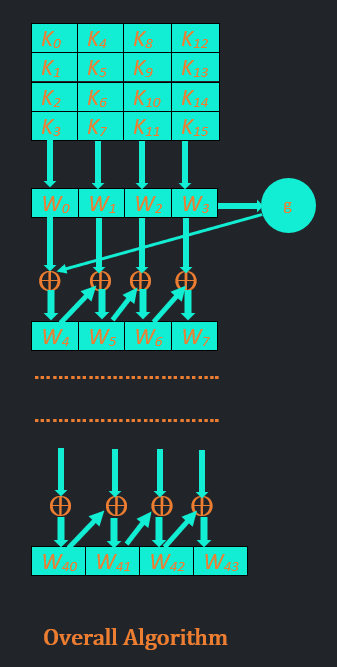
ব্যাখ্যা : 

1.প্রতিটি key 16 বাইটের একেকটি অ্যারে, যার প্রতি 4 বাইট নিয়ে একেকটি ওয়ার্ড তৈরি করি( প্রথম for loop ), এভাবে 4টি ওয়ার্ডের একটি অ্যারে পাবো ( যেমন w0 থেকে w3 )। 

2.এবারে শেষ ওয়ার্ডটিকে g ফাংশনে ইনপুট দেবো। 

3. g ফাংশনের আউটপুটের সাথে, অ্যারের ১ম ওয়ার্ডটির XOR অপারেশন করব,বাইট বাই বাইট ( দ্বিতীয় for loop4 )। এই অপারেশনের আউটপুট, পরবর্তী ওয়ার্ড অ্যারের প্রথম ওয়ার্ড হিসেবে স্টোর করবো, যে অ্যারেটা ১ম রাউন্ডের ইনপুট দেওয়া হবে। 

4. দ্বিতীয় অ্যারের পরবর্তী ওয়ার্ডগুলো পাওয়ার জন্য আমরা সিম্পলি প্রথম অ্যারের i-তম ওয়ার্ডের সাথে, দ্বিতীয় অ্যারের (i+3)-তম ওয়ার্ডের XOR অপারেশন করব। 

এভাবে [wo-w3] key থেকে [w4-w7] key , [w4-w7] key থেকে  [w8-w11] key এবং  [w40-w43] key পর্যন্ত বাকি keyগুলো এই পদ্ধতিতে বানিয়ে ফেলবো আমরা। 

g function কীভাবে কাজ করে?

এখানে বেশ কয়েকটি কাজ সম্পাদিত হয়। 

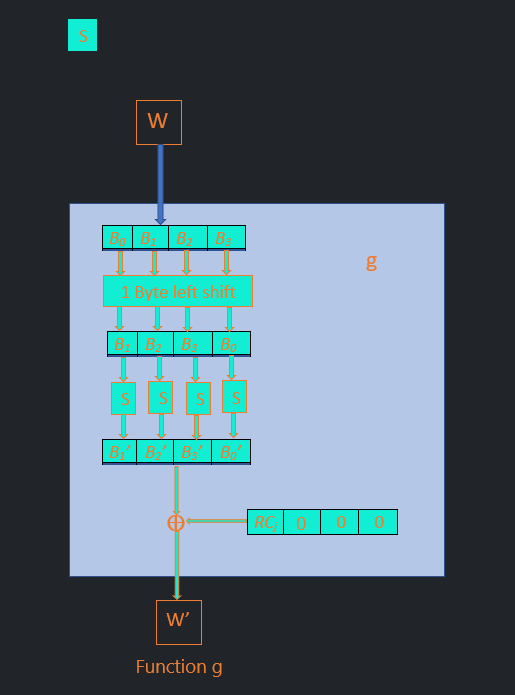
1.  ইনপুট ওয়ার্ডের বাইটগুলোকে ১ বাইট লেফট শিফট দেবো (পারমুটেশন)।

2. এবারে প্রতিটি বাইটকে একটি করে s-box  এ ইনপুট দেবো। প্রতিটি  s-box একেকটি 16X16 সাইজের টেবিল। প্রতি বাইটের প্রথম 4 বিট থেকে এর রো এবং পরবর্তী 4 বিট থেকে কলাম পজিশন পাওয়া যায়, ঐ পজিশনে থাকা এন্ট্রি দিয়ে বাইটের ভেল্যু রিপ্লেস করে ফেলবো। 

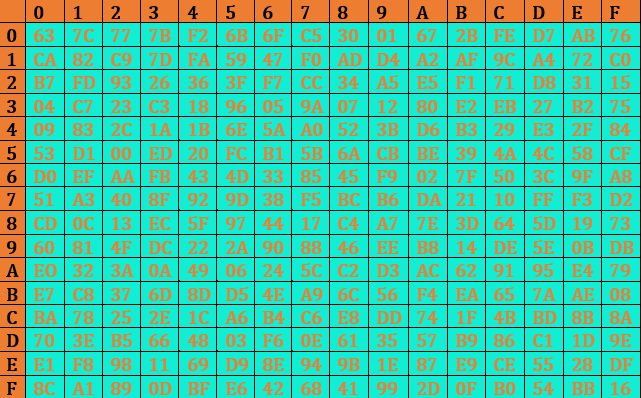
3. ধাপ-২ থেকে পাওয়া ওয়ার্ডটিকে এবার আমরা এক বিশেষ ধরনের ওয়ার্ডের সাথে XOR অপারেশন করবো,যাকে বলা হয় Round Constant(Rcon). এর সবচেয়ে বামের বাইটটি(RC[j]) ছাড়া বাকিগুলো সব শূন্য। বামের এই বাইটটির মান, রাউন্ডের উপর নির্ভরশীল। নিচের টেবিল থেকে এক নজরে দেখে নেওয়া যাক সেই মানগুলো :  

উদাহরণস্বরূপ, নবম রাউন্ডের key এর জন্য, j = 9, RC[j] = 1B. 

4. XOR অপারেশন থেকে প্রাপ্ত মানই g function এর আউটপুট। 

এবার আমরা একটি উদাহরণ দিয়ে বোঝার চেষ্টা করবো। 

ধরি, আমাদের ৫ম রাউন্ড key (in hexadecimal form) : 

13 A2 38 EB 4C 78 9D B2 92 5F 27 F7 D2 60 49 55

আমরা 6th রাউন্ড key এর সাহায্যে তৈরি করবো।   

Step-1:

6th রাউন্ড key এর প্রথম ওয়ার্ডের জন্য i = 24 

আমাদের এলগরিদম অনুসারে ২য় for লুপে, 

temp = w[i-1] = w[23] (5th রাউন্ড key এর শেষ ওয়ার্ড) 

                      = D2 60 49 55

যেহেতু  “ i mod 4 = 0 => 24 mod 4 = 0 ”  স্টেটমেন্টটি সত্য, tempকে  g function দিয়ে আপডেট করে নেবো। 

Step-2:

g function এর অপারেশনসমূহ : 

1. 1 byte লেফট শিফট : temp = leftshift(temp) = leftshift(D2 60 49 55)

                                       = 60 49 55 D2

2. s-box দিয়ে প্রতি বাইট সাবস্টিটিউশন :

    60 -> s-box -> D0

    49 -> s-box -> 3B

    55 -> s-box -> FC

    D2 -> s-box -> B5

  temp এর আপডেটেড রূপ : temp = D0 3B FC B5

3.  j = 6 এর জন্য,  RC[j] = RC[6] = 20, সুতরাং Rcon = 20 00 00 00

এখন, temp =  temp XOR Rcon

                  = D0 3B FC B5 ⊕ 20 00 00 00 

                  = F0 3B FC 85

4. g function এর আউটপুট:  temp = w’ = F0 3B FC 85

Step-3:

, w[i] = w[i-4] ⊕  temp (g function এর আউটপুট : w’) 

    => w[24] = w[20] ⊕ F0 3B FC 85 = 13 A2 38 EB ⊕ F0 3B FC 85

                  = E3 99 C4 6E

বাকি ওয়ার্ডগুলোর জন্য, “ i mod 4 =0 ” স্টেটমেন্টটি মিথ্যা,তাই tempকে  g function দিয়ে আপডেট করার প্রয়োজন নেই :

 w[25] = w[21] ⊕ w[24] =   4C 78 9D B2 ⊕ E3 99 C4 6E 

                                      = AF E1 59 DC

 w[26] = w[22] ⊕ w[25] =   92 5F 27 F7 ⊕ AF E1 59 DC   

                                      =   3D BE 7E 2B                                  

 w[27] = w[23] ⊕ w[26] =   D2 60 49 55 ⊕ 3D BE 7E 2B 

                                      = EF DE 37 7E

   The round key for the 6th round: 

         E3 99 C4 6E AF E1 59 DC 3D BE 7E 2B EF DE 37 7E

 এভাবে আমরা প্রতিটি রাউন্ডের জন্য প্রয়োজনীয় round key তৈরি করে ফেলব।