কেন ব্যবহার করব এলিপটিক কার্ভ ক্রিপ্টোগ্রাফিক (ECC) সিস্টেম?
এর উত্তর আমরা RSA(Rivest-Shamir-Adleman) এর সাথে তুলনা করে খোঁজার চেষ্টা করব । Asymmetric ক্রিপ্টোগ্রাফিতে RSA একটি গুরুত্বপূর্ণ অ্যালগরিদম, কিন্তু এর মূল সমস্যা হলো এর গাণিতিক বৈশিষ্ট্য। RSA অ্যালগরিদমে key তৈরিতে নিরাপত্তার জন্য বড় বড় যে মৌলিক সংখ্যা দুটি নির্বাচন করা হয় এবং যে এক্সপনেন্ট(সূচক) ব্যবহার করে এনক্রিপশন ও ডিক্রিপশন করা হয়, সেগুলোর মডুলার অপারেশন গাণিতিকভাবে সিস্টেমের জন্য সময়সাপেক্ষ। তার মানে আমরা যদি গাণিতিক অপারেশনের সময় কমাতে চাই, আমাদের key সাইজ অবশ্যই ছোট হওয়া চাই, কিন্তু সেটা করতে গেলে সিস্টেমের জন্য পর্যাপ্ত নিরাপত্তার ব্যবস্থা করা যাবে না, আর এখানেই আসে এলিপটিক কার্ভের প্রয়োজনীয়তা।
National Institute of Standards and Technology(NIST) এর মতে, ECC এর মাত্র 163 বিট সাইজের key, RSA এর 1024 বিট সাইজের বিশাল key এর সমতূল্য নিরাপত্তা দিতে সক্ষম!
এলিপটিক কার্ভের কিছু প্রাথমিক কথাঃ
ক্রিপ্টোগ্রাফিতে যাওয়ার আগে আমরা এলিপটিক কার্ভ সম্পর্কে কিছু প্রাথমিক ধারণা নেব, যাতে পরবর্তীতে ক্রিপ্টোগ্রাফিতে ব্যবহৃত বিভিন্ন কন্সেপ্ট সহজে বোঝা যায়।
আমরা জানি, যেকোনো জিওমেট্রিক শেইপকে এক বা একাধিক চলকের ফাংশনের মাধ্যমে প্রকাশ করা যায়, তেমনি এলিপটিক কার্ভকেও x আর y এর নিম্নোক্ত ফাংশনের আলোকে প্রকাশ করা যায়ঃ
y^2 = x^3 + ax + b ………………(1)
যেখানে x,y,a,b সবাই বাস্তব সংখ্যা। এই কার্ভ দুই ধরনের হতে পারে, সিঙ্গুলার আর নন-সিঙ্গুলার। ক্রিপ্টোগ্রাফিতে সাধারণত নন-সিঙ্গুলার কার্ভ ব্যবহার করা হয়, যে কার্ভ নিচের শর্তটি মেনে চলেঃ
4a^3 + 27b^2 ≠ 0 ……………(2)
কিন্তু বাস্তব সংখ্যার বিশাল সেট নিয়ে কাজ করা দুরূহ বলে আমরা প্রাইম সংখ্যার সেট Zp ব্যবহার করব, যেখানে যেকোনো প্রাইম সংখ্যা p এর জন্য ঐ সেটে 0 থেকে p-1 পর্যন্ত সেইসব সংখ্যা বর্তমান, যারা p এর সাথে সহমৌলিক (অর্থাৎ Zp এর প্রতিটি সদস্যের সাথে p এর 1 ছাড়া কোনো সাধারণ ফ্যাক্টর নেই) ; ফলে আমাদের কার্ভ ইকুয়েশন দাঁড়াবেঃ
y^2 ≡ x^3 + ax + b mod p ………………(3)
যেখানে x,y,a,b সকলেই Zp এর সদস্য। এই নতুন ইকুয়েশনটিকে আমরা বলব “প্রাইম কার্ভ” । একইভাবে ইকুয়েশন (২) হবেঃ
4a^3 + 27b^2 ≢ 0 mod p ………………(4)
ইকুয়েশন (3) কে লিখতে পারিঃ
y^2 mod p = (x^3 + ax + b) mod p
উদাহরণস্বরূপ, x,y,a,b,p এর মান 1,5,1,0,23 দিয়ে প্রতিস্থাপন করে পাই,
Left Hand Side = 5^2 mod 23 = 2
Right Hand Side = (1^3+1*1+0) mod 23 = 2
তার মানে এই প্রাইম কার্ভের ওপর (x,y)=(1,5) একটা পয়েন্ট। এমন সম্ভাব্য বহু পয়েন্ট থাকতে পারে।
এলিপটিক কার্ভ ক্রিপ্টোগ্রাফিঃ ডিফি-হেলম্যান কী এক্সচেঞ্জ
প্রাইম কার্ভের দুটো পয়েন্টের যোগ-বিয়োগ-গুণ, সাধারণ বীজগাণিতিক নিয়মে হয় না, এর জন্য বিশেষ কিছু অ্যালগরিদম অনুসরণ করা হয় (আলোচনার সরলীকরণের জন্য এখানে বিস্তারিত বলা হলো না), নিচের উদাহরণ থেকে তা স্পষ্ট হবে।
কার্ভের ওপর যেকোনো পয়েন্ট P = (11,10) হলে, এর ২,৩,৮,৫,৬ এর গুণিতক পাওয়া যায় যথাক্রমেঃ
2P = (13, 18)
3P = (15, 20)
4P = (9, 18)
5P = (19, 22)
6P = (1, 5)
সাধারণভাবে আমরা লিখতে পারি, k x P = R , যেখানে k = বিচ্ছিন্ন লগারিদম (discrete logarithm), P ও R = কার্ভের ওপর দুটো বাস্তব পয়েন্ট। মজার ব্যাপার হলো, এই k-ই আমাদের এলিপটিক কার্ভ ক্রিপ্টোগ্রাফির মূল হাতিয়ার! যেহেতু সাধারণ বীজগাণিতিক যোগ-বিয়োগ-গুণের নিয়ম এখানে খাটে না, তাই এমনকি কার্ভের ওপর দুটো জানা পয়েন্ট থেকেও k এর মান সরাসরি ব্রুটফোর্স আক্রমণের মাধ্যমে বের করা অসম্ভব।
ধরি জিব্রান, আরশির কাছে একটি এনক্রিপটেড ম্যাসেজ পাঠাতে চায়। এই কাজটি করার জন্য অবশ্যই পাবলিক key জেনারেট এবং বিনিময় করতে হবে।
1. দুজনে মিলে একটি বেশ বড়সড় প্রাইম সংখ্যা p নির্বাচন করবে, যার সেট হবে Zp.
2. এরপর তারা Zp এর মধ্য থেকে এমনভাবে a,b এবং কার্ভের ওপর একটি পয়েন্ট P(x,y) নির্বাচন করবে যা প্রাইম কার্ভকে সিদ্ধ করে।
3. ধরি, জিব্রান ও আরশি দুজনেই নিজেদের প্রাইভেট key ঠিক করে ফেলেছে, জিব্রানের key হলো m, আরশির key হলো n.
4. এবার দুজনেই নিজেদের প্রাইভেট key আর নির্বাচিত পয়েন্ট থেকে পাবলিক key তৈরি করে ফেলবেঃ
জিব্রানের পাবলিক key: PUj = m x P
আরশির পাবলিক key: PUa = n x P
5. এরপর তারা নিজেদের পাবলিক key পরস্পররের সাথে বিনিময় করবে। জিব্রান যখন আরশির পাবলিক key পাবে, তখন সেটা দিয়ে সে একটা key, K জেনারেট করবে, যেখানে K = m × PUa । একই কায়দায় আরশিও জিব্রানের পাবলিক key, PUj থেকে অভিন্ন key, K জেনারেট করতে পারবে, যেখানে K = n x PUj ।
এখন প্রশ্ন জাগতেই পারে, গাণিতিকভাবে দুজনের key সত্যিই কী সমান হবে?
উত্তর হলো, হ্যাঁ। জিব্রানের তৈরি করা key K-কে আমরা এভাবে লিখতে পারিঃ
K = m x PUa = m x (n x P) = n x (m x P) = n x PUj = আরশির তৈরি করা key.
আগেই বলা হয়েছে, বিচ্ছিন্ন লগারিদমের মান বের করা প্রায় অসম্ভব একটি কাজ । অ্যাটাকার যদি এমনকি কার্ভের পয়েন্ট P এবং যেকোনো একজনের পাবলিক key, ধরে নিলাম জিব্রানের পাবলিক key PUj পেয়েও যায়, সেখান থেকে তার প্রাইভেট key, m সহজে বের করতে পারবে না, কারণ m হলো বিচ্ছিন্ন লগারিদম। একই কথা আরশির বেলাতেও প্রযোজ্য।

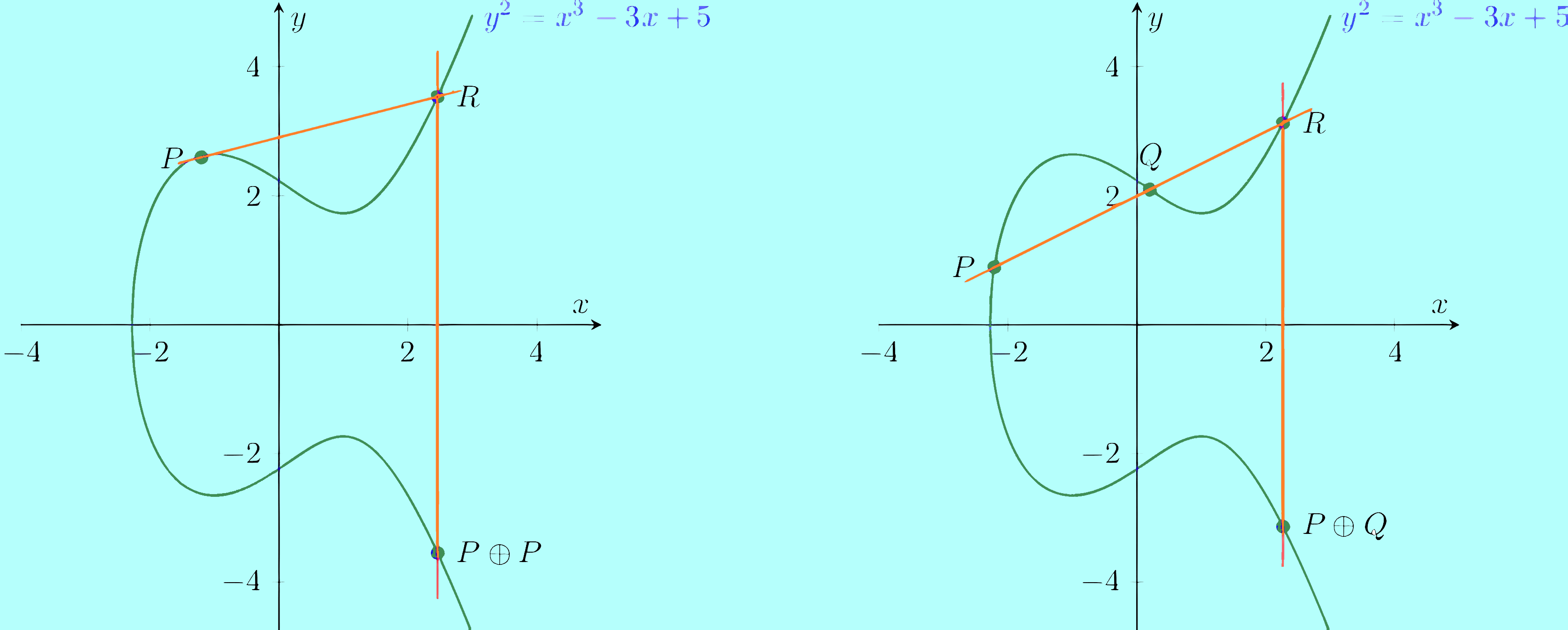

Leave a Reply