Substitution ciphertext এ প্রতিটা alphabet এর জায়গায় একটা ভিন্ন alphabet বসানো হয় । এখানে কোন সূত্রের প্রয়োগ করে alphabet এর mapping হবে এর উপর ভিত্তি করে substitution ciphertext
কয়েক প্রকার এর হতে পারে । এখানে আমরা Monoalphabetic Cipher এবং Polyalphabetic Cipher দেখব ।
Monoalphabetic Cipher
এখানে প্রতিটি alphabet এর জায়গায় ভিন্ন একটি alphabet mapping হবে । অতএব যত জায়গায় ওই alphabet থাকবে এর , বদলে শুধুমাত্র এর mapping করা alphabet ই থাকবে ।
Additive Cipher or Caeser Cipher
ciphertext = (plane text + k) mod 26 ( যেহেতু ইংরেজি বর্ণমালা ২৬ টি ) ।
plane text = ( ciphertext – k ) mod 26
k এর মান ১ থেকে ২৫ পর্যন্ত যেকোনো টা হতে পারে ।
ধরি আমাদের plaintext হলো “ hello world “ . k = 3 নিলে আমাদের ciphertext
হবে “khoor zruog”. এখানে plaintext এর মান প্রতিটা alphabet স্বতন্ত্র ধরে নেওয়া হয় । সাধারণত আমরা ক্রম মান টা ধরে নেই ।
Multiplicative Cipher
এখানে ciphertext = (plane text *k) mod 26 ( যেহেতু ইংরেজি বর্ণমালা ২৬ টি ) ।
plaintext = ( ciphertext * ( k ^ -1 ) ) mod 26
k এর মান ১ থেকে ২৫ পর্যন্ত যেকোনো টা হতে পারে ।
ধরি আমাদের plaintext হলো “ hello world “ . k = 3 নিলে আমাদের ciphertext
হবে “iuccs gschp”. এখানে plaintext এর মান প্রতিটা alphabet স্বতন্ত্র ধরে নেওয়া হয় । সাধারণত আমরা ক্রম মান টা ধরে নেই ।
Affine Cipher
Affine cipher হলো additive cipher r multiplicative cipher দুইটার সংমিশ্রণ । এখানে আমরা দুইটা key ব্যবহার করব । k1 ব্যবহৃত হবে multiplicative cipher এর সাথে আর k2 ব্যবহৃত হবে additive cipher এর সাথে ।
প্রথম ধাপ এ ciphertext ধরি T. T = ( plaintext * k1 ) mod 26
দ্বিতীয় ধাপ এ ciphertext ধরি C = ( T + k2 ) mod 26
এখন অনুরুপভাবে plaintext পেতে হলে T = ( C – k2 ) mod 26 এবং
plaintext = ( T * ( k1^-1))mod 26 .
অথবা আমরা লিখতে পারি C = ( plaintext * k1 +k2 ) mod 26 এবং
plaintext = ( ( C – k2 ) * (k1^-1) ) mod 26
উদাহরণ হিসেবে “hello” এর জন্য k1 = 7 এবং k2 = 2 ধরে পাই
h = ( 7 * 7 +2 ) mod 26 = 25 = z ( a=0 থেকে শুরু করে )
e = ( 4 * 7 + 2 ) mod 26 = 4 = e
l = ( 11 * 7 + 2 ) mod 26 = 1 = b
l = ( 11 * 7 + 2 ) mod 26 = 1 = b
o = ( 14 * 7 + 2 ) mod 26 = 22 = w
additive cipher ( “hello” ) = “zebbw”
Polyalphabetic Cipher
এখানে কোনো একটা text এ যেকোনো alphabet এর প্রতিটা occurrence এর ক্ষেত্রে ভিন্ন ভিন্ন mapping করা alphabet পাবো । যেমন আমরা “hello” এর জন্য পেতে পারি “iijvs” এখানে “hello” এর দুইবার “l” এর ভিন্ন mapping হয়েছে । এটাকেই polyalphabetic cipher বলে । Polyalphabetic cipher এর মধ্যে আছে
– Autokey cipher
– Vigenere cipher
– Playfair cipher
– Hill cipher
Vigenere Cipher
এখানে একটা plaintext এবং একটা key word দেওয়া থাকবে । ওখান থেকে আমরা ciphertext বের করব ।
Ci = ( Pi + Ki ) mod 26
এখানে Pi,Ki এবং Ci হলো plaintext , key word এবং ciphertext এর i তম বর্ণ ( যেখানে i = 0,1,2,3,…, word length পর্যন্ত ) ।

Autokey Cipher
Autokey cipher অনেকটাই vigenere cipher এর মত । তবে vigenere এর সাথে এর পার্থক্য হলো vigenere cipher এ key এর length plaintext এর সমান হয় কিন্তু auto key তে key word এর length plaintext এর সমান হয় না । তাই এর ক্ষেত্রে key এর পর থেকে যতটুকু জায়গা খালি আছে । ততটুকু জায়গায় plaintext এর alphabet গুলা বসাতে থাকব ।

এখানে আমাদের plaintext হচ্ছে “ wearediscoveredsaveyourself ” আর key word হলো “
plaintext এর alphabet গুলা পর্যায়ক্রমে বসাতে থাকব যতক্ষণ না key word এর length plaintext এর length এর সমান হয় । তাহলে আমাদের নতুন key word দাঁড়ায় “ deceptivewearediscoveredsav “ । বাকি কাজ vigenere cipher এর মত অর্থাৎ
Ci = ( Pi + Ki ) mod 26
এখানে Pi,Ki এবং Ci হলো plaintext , key word এবং ciphertext এর i তম বর্ণ ( যেখানে i = 0,1,2,3,…, word length পর্যন্ত ) । এখানে আমরা পর্যায়ক্রমে প্রতিটা আলফাবেট বসালে সাইফার টেক্সটটা পেয়ে যাব ।
Playfair Cipher
অন্যান্য ciphertext এর চেয়ে playfair ciphertext টা একটু জটিল । এখানে আমরা ধাপে ধাপে playfair ciphertext বর্ণনা করব । এখানে আমরা একটা একটা করে alphabet encrypt না করে এক জোড়া করে alphabet encrypt করব ।
১. প্রথমত আমরা একটা plaintext নেই “ instruments “ এবং key word নেই “ monarchy “ । এখন একটি ( ৫ x ৫ ) ম্যাট্রিক্স নেই যেখানে ২৫ টা alphabegt থাকবে । প্রতিটা alphabet একবার করে থাকবে । যেহেতু ইংরেজি তে বর্ণমালা ২৬ টা তাই এখানে j উহ্য থাকে । আর যদি plaintext এ j থাকে তাহলে j এর বদলে i উহ্য থাকে । এখানে আরেকটি ব্যাপার আছে । key এর ক্ষেত্রে key এর প্রতিটা alphabet unqiue হতে হবে আর ম্যাট্রিক্স এর প্রথম দিকে key এর alphabet গুলা থাকবে এরপর বাকি alphabet গুলা পর্যায়ক্রমে বসতে থাকবে ।
2. এখন আমরা plaintext থেকে ciphertext এ আনতে নিয়মগুলো জানব । – plaintext থেকে প্রতিবার দুইটা করে alphabet নিব । এখানে যেই জোড়া alphabet নিব সেই alphabet গুলা ভিন্ন থাকতে হবে । যেমন – “instrument” এর ক্ষেত্রে আমরা প্রতিবার এ দুইটা করে বর্ণ নিয়ে পাই “in” , “st” , “ru” , “me” , “nt” । আবার কখনো যদি জোড়া না মিলে তাহলে একটা “ bogus alphabet ” নিতে হবে । যেমন – “instruments” এর জন্য জোড়া গুলা হবে “in” , “st” , “ru” , “me”, “nt”, “sz” এখানে “z” হলো bogus alphabet । অনেক সময় এক ই জোড়ায় আমরা দুইটা একই alphabet পেয়ে যাই । এক্ষেত্রে তখন একটা alphabet এর পর আরেকটা bogus alphabet দিতে হবে । যেমন – “hello” এর ক্ষেত্রে জোড়া গুলো হবে “he” , “lx” , “lo” এখানে x একটি bogus alphabet ।
3.এনক্রিপ্ট করার তিনটা নিয়ম আছে ।
– যখন কোনো জোড়ার alphabet দুইটি একই রো তে থাকে ।
উদাহরণ হিসেবে আমাদের plaintext এর “st” অংশ । ম্যাট্রিক্স এ s এবং t একই রো তে আছে । এরকম জোড়ার ক্ষেত্রে আমরা প্রতিটা alphabet এর এক ঘর ডান এর alphabet নিব আর যদি alphabet টা একদম ডান পাশের টা হয় তাহলে আমরা ওই রো এর একদম বাম পাশের alphabet টা নিব । এখন s এর জায়গায় নিয়ম অনুযায়ি বসবে t আর t এর জায়গায় নিয়ম অনুযায়ি বসবে l । তাহলে “st” এর বদলে বসবে “tl”। নিচের ছবিতে যেমন ভাবে দেওয়া আছে ।
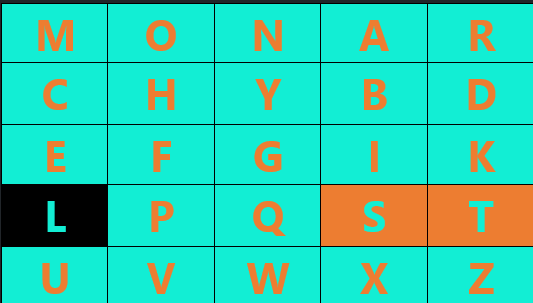
-যদি কোনো জোড়ার alphabet একই কলামে থাকে ।
উদাহরন হিসেবে plaintext এর “me” অংশ । এখানে m এবং e একই কলাম এ আছে তাই আমরা এখানে প্রতিটা alphabet এর নিচের alphabet টা নিব । m এর ক্ষেত্রে নিব c এবং e এর ক্ষেত্রে নিব l যদি plaintext এর alphabet টা একদম নিচে থাকে তাহলে আমরা ওই কলাম এর সবচেয়ে উপরের alphabet টা নিব । এখন “me” এর ciphertext “cl” ।

– উপরের দুইটি নিয়মের কোনোটিই না মানলে আমরা rectangular method ব্যবহার করব । এখানে plaintext এর ব্যবহৃত কোনো alphabet ই একই কলাম কিংবা একই রো তে থাকবে না । উদাহরন হিসেবে বলা যায় “nt” এখানে n এবং t কোনোটাই একই রো কিংবা একই কলাম এ নেই । তাই এখানে n কে একটা আয়তক্ষেত্রের প্রথম বিন্দু আর t কে আয়তক্ষেত্রের চতুর্থ বিন্দু ধরে নেই । তাহলে n এর যায়গায় বসাব r অর্থাৎ n এর রো বরাবর t এর কলাম এর alphabet আর t এর জায়গায় বসাব q অর্থাৎ t এর রো বরাবর n এর কলাম এর alphabet। এভাবে “nt” এর ciphertext হলো “rq” ।

এনক্রিপ্ট করার এই তিনটা নিয়ম আর জোড়া বানানোর নিয়মগুলা মেনে “monarch” key word আর “instruments” plaintext এর playfair cipher encription নিচে দেখানো হলো ।
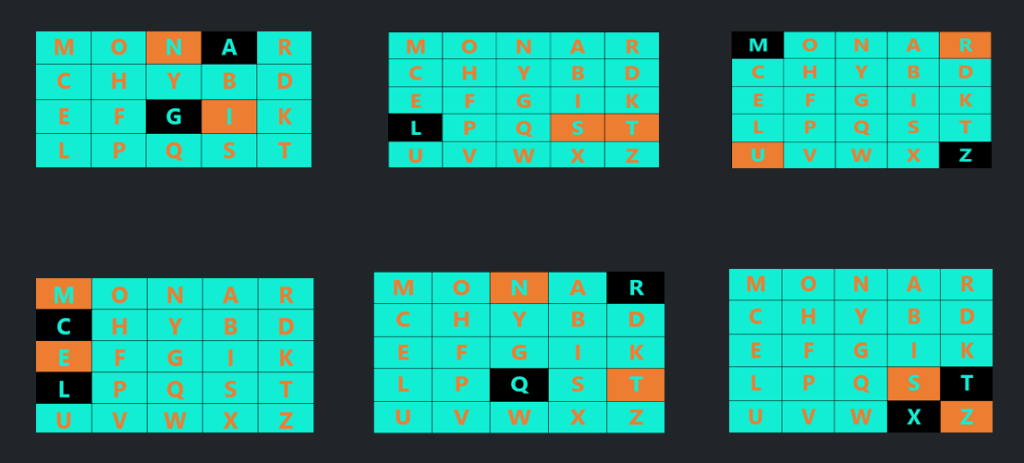
[source: https://www.geeksforgeeks.org/playfair-cipher-with-examples/]
Hill Cipher
এখানে আমরা একটা plaintext নিব । ধরি plaintext এ n টি alphabet আছে তাই আমরা n x n টি alphabet এর একটি key নিব । উদাহরন হিসেবে plaintext “act” যেটা 3 alphabet এর এবং key “gybnqkurp” যেটা 3 x 3 এর একটি key । এখন আমরা key নিয়ে একটি 3 x 3 এর একটি ম্যাট্রিক্স নিব যেখানে key এর alphabet গুলা পর্যায়ক্রমে সাজানো থাকবে ।

এবার আমরা আরেকটা ম্যাট্রিক্স নিব ( 3 x 1 ) এর এবং key এর ম্যাট্রিক্স এবং দ্বিতীয় ম্যাট্রিক্স গুন করে দিব ।

এদের গুনফল ম্যাট্রিক্স কে 26 দিয়ে mod করলেই আমরা ciphertext পেয়ে যাব ।
নিচের ম্যাট্রিক্স থেকে আমরা পাই plaintext = “act” ,
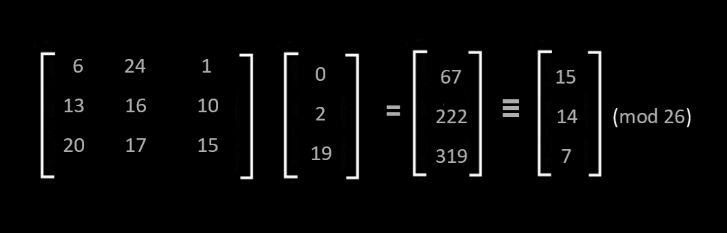



Leave a Reply