RSA(Rivest-Shamir-Adleman)

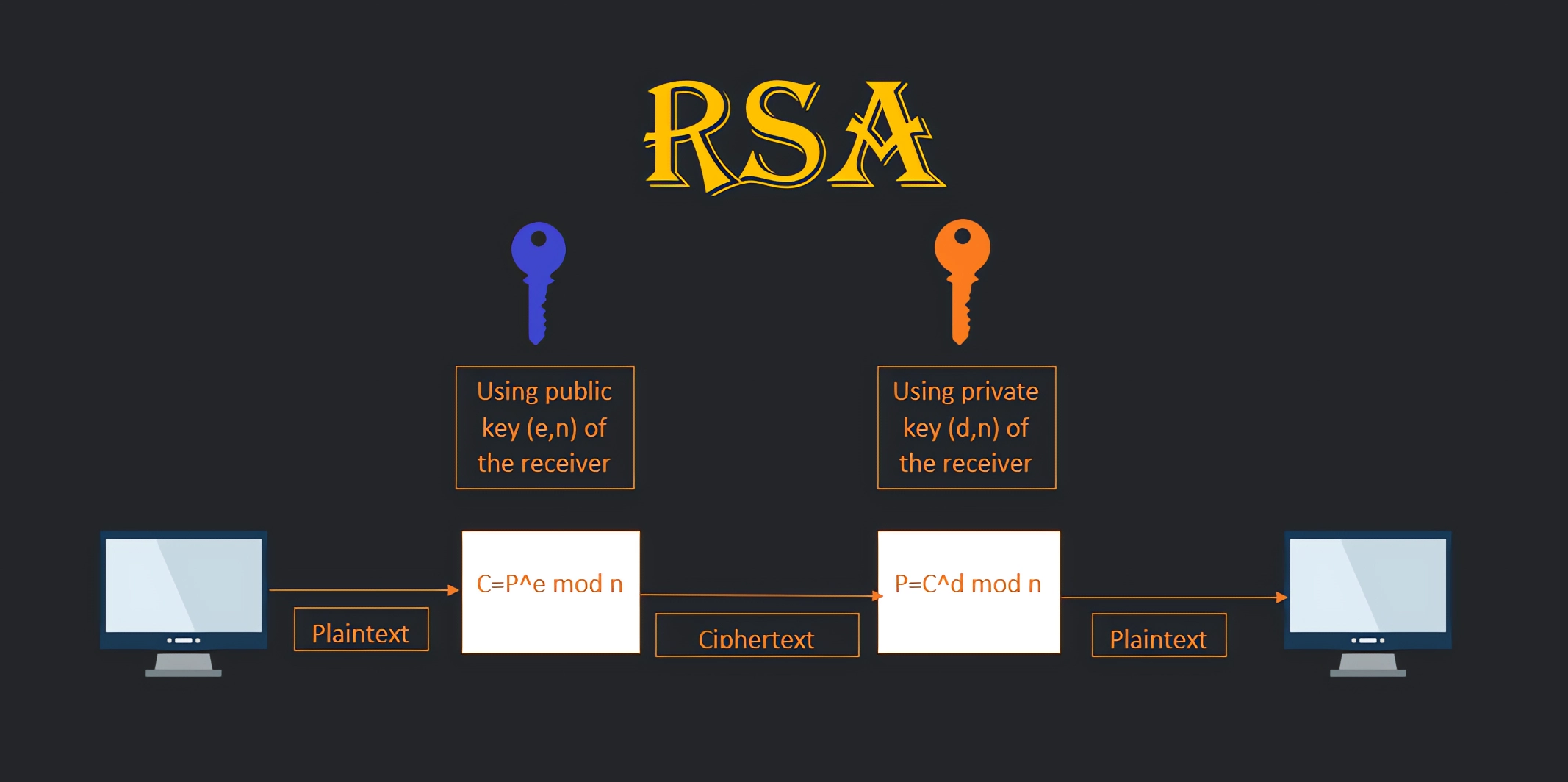
RSA একটি asymmetric key এলগরিদম যেটা এনক্রিপশন এবং ডিজিটাল সিগনেচার এ ব্যবহৃত হয়। এখানে আমরা দুইটা বড় প্রাইম সংখ্যা নিয়ে কাজ করব। এই এলগরিদমটি তিনটি ভাগ এ ভাগ করে কাজ করে ।

Key Generation

যেকোনো দুইটা বড় প্রাইম সংখ্যা নেই। উদারহণ হিসেবে a=61,b=53 ধরি।

n=a*b

=61*53

=3233

এখন আমাদের কে ইউলার এর টশেন্ট ফাংশন বের করতে হবে n এর জন্য । অর্থাৎ 1 থেকে n পর্যন্ত কতগুলা সংখ্যা n এর সাথে কো-প্রাইম হবে সেটা । টশেন্ট ফাংশন φ(n)=(a-1)*(b-1)=60*52=3120।

এখন একটি পাবলিক এক্সপনেন্ট লাগবে (যেটা φ(n) এর সাথে কো-প্রাইম হবে)। ধরি সংখ্যা টা e=17.

এবারে আমরা একটা প্রাইভেট এক্সপনেন্ট d এমনভাবে বের করব যেন d * e ≡ 1 ( mod φ ( n ) ) হয় । এখানে আমাদের d=2753 আসে। এখন আমাদের public key=( e , n ) = ( 17 , 3233 ) এবং private key = ( 2753 , 3233 ) ।

Encryption

ধরি আপনি একটি ম্যাসেজ পাঠাতে চাচ্ছেন । ধরি ম্যাসেজটি “Hello!” এখানে H এর মান ধরি H = 123 . এই অনুযায়ী এনক্রিপশন ফর্মুলা হচ্ছে C ≡ H ^e (mod n) । মানগুলা বসিয়ে পাই

C ≡ 123^17 (mod 3233)

C ≡ 2924 (mod 3233)

অতএব এনক্রিপ্টেড ম্যাসেজটি হল 2924

Decryption

এখানে ডিক্রিপশন ফর্মুলা হচ্ছে

H ≡ C^d (mod n) , মান বসিয়ে পাই

H ≡ 2924^2753 (mod 3233)

H ≡ 123 (mod 3233)

অতএব ডিক্রিপ্টেড ম্যাসেজটি হল 123 । অর্থাৎ H মান আগের মানের সাথে মিলে গেছে।

RSA এলগরিদম এ প্রাইম সংখ্যা দুইটা যত বড় হবে ডাটা ততবেশি সিকিউরড হবে । RSA এর সিকিউরিটি মূলত নির্ভর করে n কে কিভাবে এর প্রাইম ফ্যাক্টর ( a and b )তে ভাঙ্গানো যায় । n এর মান যত বড় এর জন্য কাঙ্খিত ( a ও b ) পাওয়া তত কঠিন ।

নিচে এর পাইথন কোড দেওয়া হলোঃ

        
from cryptography.hazmat.primitives import serialization
from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives.asymmetric import padding
from cryptography.hazmat.primitives import hashes

def generate_key_pair():
    # Generate an RSA key pair
    private_key = rsa.generate_private_key(
        public_exponent=65537,
        key_size=2048,
        backend=default_backend()
    )

    # Get the public key
    public_key = private_key.public_key()

    # Serialize and return the keys
    private_key_bytes = private_key.private_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PrivateFormat.PKCS8,
        encryption_algorithm=serialization.NoEncryption()
    )

    public_key_bytes = public_key.public_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PublicFormat.SubjectPublicKeyInfo
    )

    return private_key_bytes, public_key_bytes

def encrypt(message, public_key):
    # Load the public key
    public_key = serialization.load_pem_public_key(public_key, backend=default_backend())

    # Encrypt the message
    ciphertext = public_key.encrypt(
        message.encode('utf-8'),
        padding.OAEP(
            mgf=padding.MGF1(algorithm=hashes.SHA256()),
            algorithm=hashes.SHA256(),
            label=None
        )
    )

    return ciphertext

def decrypt(ciphertext, private_key):
    # Load the private key
    private_key = serialization.load_pem_private_key(private_key, password=None, backend=default_backend())

    # Decrypt the ciphertext
    decrypted_message = private_key.decrypt(
        ciphertext,
        padding.OAEP(
            mgf=padding.MGF1(algorithm=hashes.SHA256()),
            algorithm=hashes.SHA256(),
            label=None
        )
    )

    return decrypted_message.decode('utf-8')

# Example usage:
private_key, public_key = generate_key_pair()

message = "Hello, RSA!"
print(f"Original message: {message}")

ciphertext = encrypt(message, public_key)
print(f"Ciphertext: {ciphertext}")

decrypted_message = decrypt(ciphertext, private_key)
print(f"Decrypted message: {decrypted_message}")

Share on:

Category:

Asymmetric